Tuliskan bilangan bulat yang kurang dari 3 – Dalam dunia matematika, bilangan bulat memegang peranan penting. Di antara bilangan bulat tersebut, terdapat kelompok bilangan yang lebih kecil dari 3. Kelompok bilangan ini memiliki sifat dan keunikan yang menarik untuk dibahas.
Tulisan ini akan mengajak Anda menyelami dunia bilangan bulat yang kurang dari 3. Kita akan mengeksplorasi pengertiannya, operasi yang dapat dilakukan, dan aplikasinya dalam kehidupan sehari-hari.
Bilangan Bulat: Pengertian dan Karakteristik

Bilangan bulat adalah angka yang tidak memiliki bagian pecahan atau desimal. Mereka dapat berupa bilangan positif (lebih besar dari 0), bilangan negatif (kurang dari 0), atau nol.
Contoh Bilangan Bulat
Beberapa contoh bilangan bulat adalah:
- 5
- -3
- 0
- 100
- -50
Perbedaan antara Bilangan Bulat dan Bilangan Riil, Tuliskan bilangan bulat yang kurang dari 3
Bilangan bulat berbeda dengan bilangan riil, yang dapat memiliki bagian pecahan atau desimal. Misalnya, 3,5 dan
2,7 adalah bilangan riil tetapi bukan bilangan bulat.
Bilangan Bulat Kurang dari 3: Tuliskan Bilangan Bulat Yang Kurang Dari 3
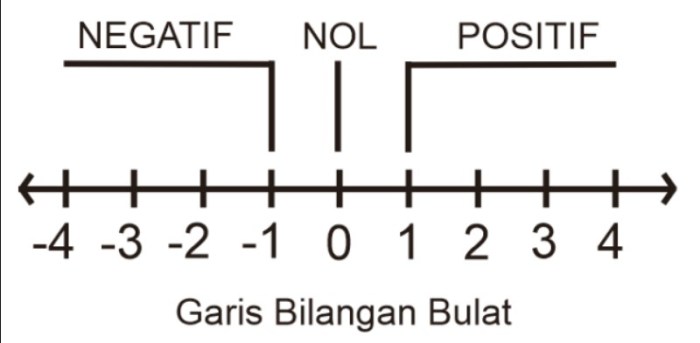
Dalam matematika, bilangan bulat adalah himpunan angka yang mencakup bilangan asli (1, 2, 3, …), nol (0), dan bilangan negatif (-1, -2, -3, …). Bilangan bulat yang kurang dari 3 adalah bilangan bulat yang lebih kecil dari 3.
Daftar Bilangan Bulat Kurang dari 3
- -2
- -1
- 0
Tabel Bilangan Bulat Kurang dari 3
| Bilangan | Nilai |
|---|---|
| -2 | Lebih kecil dari 3 |
| -1 | Lebih kecil dari 3 |
| 0 | Lebih kecil dari 3 |
Operasi pada Bilangan Bulat Kurang dari 3
Bilangan bulat kurang dari 3 adalah
- 2,
- 1, 0, 1, dan 2. Operasi dasar pada bilangan bulat ini meliputi penjumlahan, pengurangan, perkalian, dan pembagian.
Penjumlahan
Penjumlahan bilangan bulat kurang dari 3 mengikuti aturan berikut:
- -2 + (-1) = -3
- -2 + 0 = -2
- -2 + 1 = -1
- -2 + 2 = 0
- -1 + (-1) = -2
- -1 + 0 = -1
- -1 + 1 = 0
- -1 + 2 = 1
- 0 + (-1) = -1
- 0 + 0 = 0
- 0 + 1 = 1
- 0 + 2 = 2
- 1 + (-1) = 0
- 1 + 0 = 1
- 1 + 1 = 2
- 1 + 2 = 3
- 2 + (-1) = 1
- 2 + 0 = 2
- 2 + 1 = 3
- 2 + 2 = 4
Pengurangan
Pengurangan bilangan bulat kurang dari 3 mengikuti aturan berikut:
- -2 – (-1) = -1
- -2 – 0 = -2
- -2 – 1 = -3
- -2 – 2 = -4
- -1 – (-1) = 0
- -1 – 0 = -1
- -1 – 1 = -2
- -1 – 2 = -3
- 0 – (-1) = 1
- 0 – 0 = 0
- 0 – 1 = -1
- 0 – 2 = -2
- 1 – (-1) = 2
- 1 – 0 = 1
- 1 – 1 = 0
- 1 – 2 = -1
- 2 – (-1) = 3
- 2 – 0 = 2
- 2 – 1 = 1
- 2 – 2 = 0
Perkalian
Perkalian bilangan bulat kurang dari 3 mengikuti aturan berikut:
- -2 × (-1) = 2
- -2 × 0 = 0
- -2 × 1 = -2
- -2 × 2 = -4
- -1 × (-1) = 1
- -1 × 0 = 0
- -1 × 1 = -1
- -1 × 2 = -2
- 0 × (-1) = 0
- 0 × 0 = 0
- 0 × 1 = 0
- 0 × 2 = 0
- 1 × (-1) = -1
- 1 × 0 = 0
- 1 × 1 = 1
- 1 × 2 = 2
- 2 × (-1) = -2
- 2 × 0 = 0
- 2 × 1 = 2
- 2 × 2 = 4
Pembagian
Pembagian bilangan bulat kurang dari 3 mengikuti aturan berikut:
- -2 ÷ (-1) = 2
- -2 ÷ 0 = Tidak terdefinisi
- -2 ÷ 1 = -2
- -2 ÷ 2 = -1
- -1 ÷ (-1) = 1
- -1 ÷ 0 = Tidak terdefinisi
- -1 ÷ 1 = -1
- -1 ÷ 2 = -0,5
- 0 ÷ (-1) = 0
- 0 ÷ 0 = Tidak terdefinisi
- 0 ÷ 1 = 0
- 0 ÷ 2 = 0
- 1 ÷ (-1) = -1
- 1 ÷ 0 = Tidak terdefinisi
- 1 ÷ 1 = 1
- 1 ÷ 2 = 0,5
- 2 ÷ (-1) = -2
- 2 ÷ 0 = Tidak terdefinisi
- 2 ÷ 1 = 2
- 2 ÷ 2 = 1
Sifat-sifat operasi pada bilangan bulat kurang dari 3 meliputi:*
-*Komutatif
Penjumlahan dan perkalian bersifat komutatif, artinya urutan operasi tidak memengaruhi hasil.
-*Asosiatif
Penjumlahan dan perkalian bersifat asosiatif, artinya pengelompokan operasi tidak memengaruhi hasil.
- 1 adalah invers penjumlahan untuk setiap bilangan bulat kurang dari 3, dan 1 adalah invers perkalian untuk setiap bilangan bulat kurang dari 3 selain 0.
-*Distributif
Perkalian mendistribusikan terhadap penjumlahan.
-*Identitas
0 adalah identitas penjumlahan, dan 1 adalah identitas perkalian.
-*Invers
Aplikasi Bilangan Bulat Kurang dari 3
Bilangan bulat kurang dari 3, yakni -2, -1, dan 0, mungkin tampak sederhana, namun mereka memiliki aplikasi yang luas dalam berbagai bidang kehidupan sehari-hari.
Matematika
Dalam matematika, bilangan bulat kurang dari 3 berperan penting dalam:
- Operasi dasar: Penjumlahan, pengurangan, perkalian, dan pembagian
- Teori bilangan: Sebagai bilangan prima (-1) dan komposit (-2, 0)
- Geometri: Menentukan posisi titik pada garis bilangan
Sains
Dalam sains, bilangan bulat kurang dari 3 digunakan dalam:
- Fisika: Sebagai besaran negatif (misalnya, suhu di bawah nol)
- Kimia: Menunjukkan valensi ion (misalnya, -2 untuk oksigen)
- Biologi: Sebagai indikator pertumbuhan (misalnya, pertumbuhan negatif pada organisme)
Teknologi
Dalam teknologi, bilangan bulat kurang dari 3 diterapkan dalam:
- Komputer: Sebagai nilai biner (0 dan -1)
- Pemrograman: Sebagai nilai boolean (true dan false)
- Jaringan: Sebagai indikator status (misalnya, -1 untuk kesalahan)