Persamaan Kuadrat: Temukan Akar yang Tersembunyi di Balik Angka 6

Dalam dunia matematika, persamaan kuadrat yang akar akarnya dan 6 adalah merupakan sebuah teka-teki yang menggugah pikiran. Persamaan ini tidak hanya menguji keterampilan aljabar kita, tetapi juga mengungkapkan keindahan simetri dan keteraturan dalam angka.

Mari kita menyelami dunia persamaan kuadrat dan mengungkap misteri di balik akar yang tersembunyi ini, serta mengeksplorasi penerapannya yang menarik dalam kehidupan sehari-hari.

Daftar isi

Persamaan Kuadrat

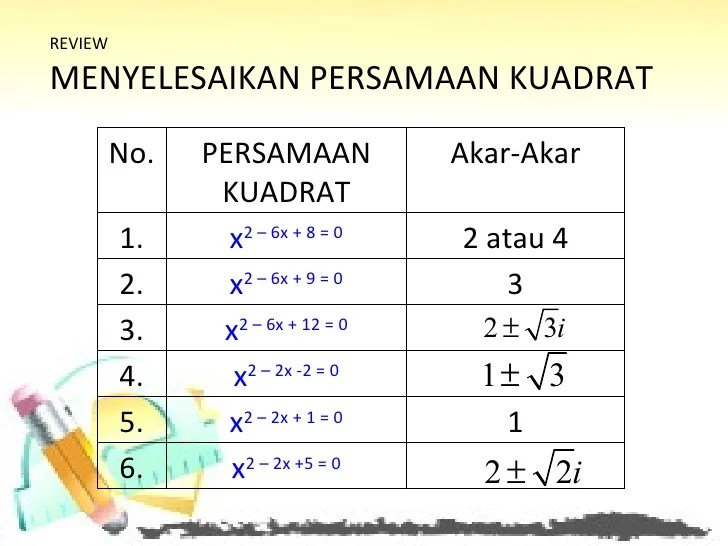
Persamaan kuadrat merupakan persamaan matematika yang memiliki bentuk umum ax ²+ bx + c = 0, di mana a, b, dan c adalah konstanta dan x adalah variabel yang ingin dicari nilainya. Persamaan kuadrat memiliki dua akar, yaitu nilai x yang memenuhi persamaan tersebut.

Salah satu cara untuk mencari akar persamaan kuadrat adalah dengan menggunakan rumus abc atau rumus kuadrat, yaitu x = (-b ± √(b ²– 4ac)) / 2a. Rumus ini diturunkan dari bentuk umum persamaan kuadrat dan membantu kita menemukan nilai x dengan mudah.

Akar Persamaan Kuadrat

Akar persamaan kuadrat adalah nilai x yang membuat persamaan menjadi benar.
Setiap persamaan kuadrat memiliki dua akar, yang bisa sama atau berbeda.
Akar persamaan kuadrat dapat ditemukan menggunakan rumus abc atau rumus kuadrat.

Contoh Persamaan Kuadrat, Persamaan kuadrat yang akar akarnya dan 6 adalah

Salah satu contoh persamaan kuadrat adalah x ²– 5x + 6 = 0. Persamaan ini memiliki akar x = 2 dan x = 3. Ini berarti bahwa nilai x yang membuat persamaan benar adalah 2 dan 3.

Penerapan Persamaan Kuadrat

Persamaan kuadrat memiliki banyak aplikasi dalam kehidupan nyata, seperti:

Mencari tinggi suatu benda dengan menggunakan persamaan gerak jatuh bebas.
Menghitung jarak yang ditempuh oleh suatu benda dengan menggunakan persamaan gerak lurus beraturan.
Membuat model fungsi kuadrat untuk menggambarkan hubungan antara dua variabel.

Mencari Akar Persamaan Kuadrat

Persamaan kuadrat adalah persamaan yang berbentuk ax² + bx + c = 0, dimana a, b, dan c adalah bilangan real dan a tidak sama dengan 0. Akar-akar persamaan kuadrat adalah nilai-nilai x yang memenuhi persamaan tersebut.

Rumus Kuadrat

Rumus kuadrat digunakan untuk mencari akar-akar persamaan kuadrat. Rumusnya adalah:

x = (-b ± √(b²
4ac)) / 2a

Dimana:

x adalah akar persamaan kuadrat
a, b, dan c adalah koefisien persamaan kuadrat

Contoh Penggunaan Rumus Kuadrat

Misalkan kita ingin mencari akar-akar dari persamaan kuadrat x² – 5x + 6 = 0. Menggunakan rumus kuadrat, kita dapat menghitung akar-akarnya sebagai berikut:

x = (-(-5) ± √((-5)² – 4(1)(6))) / 2(1)

x = (5 ± √25 – 24) / 2

x = (5 ± 1) / 2

x₁ = 2

x₂ = 3

Jadi, akar-akar dari persamaan kuadrat x² – 5x + 6 = 0 adalah x₁ = 2 dan x₂ = 3.

Persamaan Kuadrat dengan Akar 6

Dalam matematika, persamaan kuadrat merupakan persamaan polinomial derajat dua dengan bentuk umum ax² + bx + c = 0. Salah satu topik yang sering dibahas dalam persamaan kuadrat adalah persamaan kuadrat yang memiliki akar 6.

Identifikasi Persamaan Kuadrat dengan Akar 6

Persamaan kuadrat yang memiliki akar 6 memenuhi sifat bahwa salah satu akarnya adalah 6. Artinya, jika x = 6 disubstitusikan ke dalam persamaan kuadrat, maka hasilnya harus sama dengan 0.

Pembuatan Tabel Contoh Persamaan Kuadrat dengan Akar 6

Berikut adalah tabel yang menunjukkan beberapa contoh persamaan kuadrat dengan akar 6:

Persamaan Kuadrat	Akar
x² 6 = 0	6
x² 12x + 36 = 0	6
x² 2x 24 = 0	6

Persamaan Kuadrat

Akar

x²

6 = 0

x²

12x + 36 = 0

x²

2x
24 = 0

Aplikasi Persamaan Kuadrat dengan Akar 6: Persamaan Kuadrat Yang Akar Akarnya Dan 6 Adalah

Persamaan kuadrat dengan akar 6 memiliki aplikasi yang luas dalam berbagai bidang kehidupan sehari-hari. Dari arsitektur hingga fisika, persamaan ini dapat membantu kita memecahkan masalah yang melibatkan jarak, kecepatan, dan percepatan.

Penerapan dalam Arsitektur

Dalam arsitektur, persamaan kuadrat dengan akar 6 dapat digunakan untuk menentukan dimensi optimal sebuah bangunan. Misalnya, seorang arsitek mungkin ingin mendesain sebuah ruangan yang panjangnya dua kali lebarnya dan luas lantainya 60 meter persegi. Menggunakan persamaan kuadrat, mereka dapat menemukan bahwa dimensi ruangan yang memenuhi persyaratan ini adalah panjang 12 meter dan lebar 6 meter.

Penerapan dalam Fisika

Dalam fisika, persamaan kuadrat dengan akar 6 dapat digunakan untuk menghitung lintasan proyektil. Ketika sebuah benda dilempar ke udara, lintasannya mengikuti lintasan parabola yang dapat dimodelkan menggunakan persamaan kuadrat. Dengan mengetahui kecepatan awal dan sudut peluncuran, persamaan ini dapat digunakan untuk menentukan ketinggian maksimum dan jarak horizontal yang ditempuh proyektil.

Persamaan Kuadrat: Temukan Akar yang Tersembunyi di Balik Angka 6

indoaviation.co.id platform online yang berdedikasi untuk menyediakan informasi yang akurat, terkini, dan relevan dalam berbagai topik menarik seputar manfaat, Administrasi, Agama, Agama dan Kepercayaan, Agama dan Masyarakat, Agama dan Spiritualitas, Agama di Indonesia, Agama Islam, Ajaran Islam, Akhlak, Akhlak Islam, Aktivitas Fisik, Aktivitas Gerak Berirama, Aktivitas Luar Ruangan, Akustik, Alam, Alam dan Lingkungan, Alam dan Satwa Liar, Alat, Alat Musik, Alat Musik Perkusi, Alat Musik Tiup, Alat Optik, Alat Tulis, Aljabar, Amal, Analisis Anekdot, Analisis Bisnis, Analisis Data, Analisis Gambar, Analisis Musik, Analisis Narasi, Analisis Percakapan, Analisis Puisi, Analisis Sastra, Analisis Teks, Anatomi, Anatomi Kardiovaskular, Anime dan Manga, Antropologi, Antropologi Budaya, Aplikasi, Arkeologi, Arsitektur, Arsitektur Buddha, Asmaul Husna, Astronomi, Atletik, Aturan Sepak Bola, Bacaan Al-Qur'an, Bahan, Bahan Alami, Bahan Baku Tekstil, Bahan Bangunan, Bahan Kemasan, Bahan Lanjutan, Bahan Makanan, Bahan Tambahan Makanan, Bahan Tekstil, Bahasa, Bahasa Arab, Bahasa Daerah, Bahasa dan Budaya, Bahasa dan Budaya Jepang, Bahasa dan Komunikasi, Bahasa dan Linguistik, Bahasa dan Masyarakat, Bahasa dan Sastra, Bahasa Indonesia, Bahasa Inggris, Bahasa Jawa, Batik, Belajar, Belajar Efektif, Belanja, Benda Langit, Berenang, Berita dan Media, Berkebun, Berkemah dan Mendaki, Berkuda, Bernyanyi, Bibliografi, Biokimia, Biologi, Biologi Hewan, Biologi Populasi, Biologi Sel, Biologi Tumbuhan, Bioteknologi, Bisbol, Bisnis dan Ekonomi, Bisnis dan Kewirausahaan, Bisnis Pertanian, Bola Basket, Bola Voli, Botani, Branding, Buah-buahan, Budaya, Budaya Aceh, Budaya Betawi, Budaya Daerah, Budaya dan Filsafat, Budaya dan Masyarakat, Budaya dan Tradisi, Budaya Indonesia, Budaya Jawa, Budaya Kalimantan Barat, Budidaya Buah, Budidaya Hewan, Budidaya Perikanan, Bulutangkis, Bumbu dan Rempah, Cara, Ceramah dan Presentasi, Ciptaan Tuhan, Dampak Globalisasi, Dekorasi Rumah, Demokrasi, Desain Buku, Desain Grafis, Desain Interior, Desain Poster, Desain sampul buku, Desain Warna, Distribusi, Dokumen, Dokumentasi Proses, Dongeng, Dongeng dan Makna Hidup, Dunia Hewan, Ekologi, Ekologi dan Konservasi, Ekologi Tanah, Ekologi Tumbuhan, Ekonomi, Ekonomi ASEAN, Ekonomi Asia Tenggara, Ekonomi Bisnis, Ekonomi dan Bisnis, Ekonomi Global, Ekonomi Indonesia, Ekonomi Pedesaan, Ekonomi Pertanian, Ekonomi Singapura, Eksplorasi Luar Angkasa, Elektronik, Elektronika, Energi, Energi Bersih, Energi Terbarukan, Entomologi, Ergonomi, Eropa, Eskatologi Islam, Estetika, Etika, Etika dan Moral, Etika dan Moralitas, Etika dan Nilai-Nilai, Falsafah Pancasila, Fantasi, Fashion, Fashion dan Desain, Fashion dan Gaya Hidup, Fenomena Alam, Fenomena Global, Fiksi, Fiksi Ilmiah, Filosofi Hidup, Filosofi Kehidupan, Filsafat, Filsafat dan Spiritualitas, Filsafat Hidup, Filsafat Jawa, Filsafat Politik, Finishing Perabot, Fisika, Fisika Akustik, Fisika Bola, Fisika Dasar, Fisika Optik, Fisika Suara, Fisika Terapan, Fisika Termal, Fisiologi Hewan, Flora dan Fauna, Fonologi, Formulir, Fotografi, Fungsi Ekologis Hutan, Furnitur, Game Strategi, Gangguan Darah, Gangguan Pencernaan, Gaya, Genetika Manusia, Geografi, Geografi Afrika, Geografi Asia, Geografi Asia Tenggara, Geografi Jepang, Geografi Sosial, Geometri, Geometri Lingkaran, Geosains, Gerak Berirama, Gerak Tari, Gerakan Tubuh, Globalisasi, Habitat Tanaman, Hadis, Hak Asasi Manusia, Hak dan Kewajiban, Hak Kekayaan Intelektual, Hak Warga Negara, Hak-hak Asasi Manusia, Hasil Hutan, Hemat Energi, Hewan, Hewan Gurun, Hewan Liar, Hubungan, Hubungan Internasional, Hubungan Interpersonal, Hubungan Keluarga, Hubungan Sosial, Hukum, Hukum Bacaan Alquran, Hukum Bisnis, Hukum dan Masyarakat, Hukum Konstitusi, Hukum Tata Negara, Hutan, Ibadah, Ibadah dan Amaliah Keagamaan, Identitas Pribadi, Ideologi Bangsa, Iklan, Iklan dan Pemasaran, Ilmu Material, Ilmu Pengetahuan, Ilmu Pengetahuan Alam, Ilmu Pengetahuan dan Kehidupan Manusia, Ilmu Sosial, Ilmu Tajwid, Ilustrasi, Ilustrasi Digital, Iman, Industri, Industri Makanan, Industri Tekstil, Informasi dan Literasi, Infrastruktur Pejalan Kaki, Inspirasi, Interaksi Manusia, Interaksi Sosial, Interpretasi Gambar, Investasi Emas, Jujutsu Kaisen, Jurnalisme, Karakter dan Etika, Karakter Fiksi, Kartografi, Karya Sastra, Keamanan Listrik, Keamanan Siber, Kearifan Lokal, Kebanggaan Nasional, Keberagaman dan Inklusi, Keberagaman dan Integrasi, Kebersihan, Kebijaksanaan, Kebugaran, Kebugaran dan Kesehatan, Kebugaran dan Latihan, Kebugaran dan Olahraga, Kebugaran Fisik, Kebugaran Jasmani, Kebutuhan Remaja, Kegiatan Ekonomi, Kegiatan Sosial, Kehidupan, Kehidupan Beragama, Kehidupan Berbangsa dan Bernegara, Kehidupan Bermasyarakat, Kehidupan Bertetangga, Kehidupan Desa, Kehidupan Keluarga, Kehidupan Satwa Liar, Kehidupan Sehari-hari, Kehidupan Sosial, Keimanan, Keindahan Alam, Keislaman, Kekerasan Seksual, Kelestarian Lingkungan, Kelincahan Olahraga, Kelistrikan, Keluarga, Kemagnetan, Kemajemukan, Kemasan Produk, Kenabian, Kenampakan Alam, Kepedulian Sosial, Kepemimpinan, Kepemimpinan Islami, Kependudukan, Kepercayaan Agama, Kepercayaan dan Spiritualitas, Kerajinan, Kerajinan Tangan, Kerajinan Tradisional, Keramik, Kerja Sama Internasional, Kerjasama ASEAN, Kerjasama Regional, Kesehatan, Kesehatan dan Kebugaran, Kesehatan dan Keselamatan, Kesehatan dan Lingkungan, Kesehatan dan Nutrisi, Kesehatan Gigi, Kesehatan Kaki, Kesehatan Lingkungan, Kesehatan Masyarakat, Kesehatan Mental, Kesehatan Muskuloskeletal, Kesehatan Pernapasan, Kesehatan Sendi, Kesehatan Tanaman, Kesehatan Tenggorokan, Kesehatan Tulang, Kesejahteraan Hewan dan Tumbuhan, Kesejahteraan Masyarakat, Kesenian Tradisional, Ketahanan Nasional, Ketahanan Negara, Ketahanan Pangan, Keterampilan Basket, Keterampilan Berbahasa, Keterampilan Berbicara, Keterampilan Berkomunikasi, Keterampilan Komunikasi, Keterampilan Membaca, Keterampilan Menulis, Keterampilan Olahraga, Keterampilan Sepak Bola, Keuangan, Kewajiban Agama, Kewajiban dan Tanggung Jawab, Kewarganegaraan, Keyakinan Islam, Khotbah, Kimia, Kimia Anorganik, Kimia Dasar, Kimia Fisika, Kisah Alkitab, Kisah Nabi, Komunikasi, Komunikasi Digital, Komunikasi Efektif, Komunikasi Interpersonal, Komunikasi Publik, Komunikasi Verbal, Komunikasi Visual, Komunitas, Konflik, Konflik Sosial, Konservasi Alam, Konservasi Energi, Konservasi Satwa Liar, Konservasi Sumber Daya Alam, Konservasi Tanah, Konstruksi dan Bangunan, Konversi, Konversi Satuan, Konversi Unit, Konversi Waktu, Koperasi dan Pertanian, Koreografi, Koreografi Tari, Kosmologi, Kritik Sastra, Kuda-Kuda, Kuliner, Kuliner Indonesia, Kursi, Laporan Ilmiah, Lari, Lari Cepat, Lari Jarak Jauh, Lari Jarak Pendek, Latihan Fisik, Latihan Kebugaran, Latihan Kekuatan, Latihan Olahraga, Latihan Sepak Bola, Legenda, Legenda Rakyat Indonesia, Lembaga Sosial, Lilin, Limbah Industri, Lingkungan, Lingkungan dan Masyarakat, Lingkungan Hidup, Linguistik, Literasi Media, Lukisan, Mahabharata, Mainan kucing, Majas, Makanan, Makanan Cepat Saji, Makanan dan Minuman, Malaikat, Mamalia Indonesia, Manajemen Acara, Manajemen Bisnis, Manajemen Data, Manajemen Diri, Manajemen Keuangan, Manajemen Kualitas, Manajemen Organisasi, Manajemen Pameran, Manajemen Pelayanan, Manajemen Perubahan, Manajemen Waktu, Manajemen Wawancara, Manfaat, Manfaat Membaca, Manufaktur, Manusia dan Masyarakat, Masakan Indonesia, Masalah Sosial ASEAN, Masyarakat, Mata Uang, Matematika, Matematika Dasar, Media Elektronik, Media Seni Musik, Melukis, Memahami Teks, Memasak, Membaca dan Menulis, Menembak, Menggambar, Menggambar Komik, Menulis, Menulis Cerpen, Menulis Kreatif, Metabolisme Hewan, Metalurgi, Meteorologi, Metodologi Penelitian, Migrasi, Mineral dan Penambangan, Miniatur, Mitologi Hindu, Moralitas, Motif Ekonomi, Motif Geometris, Motivasi Diri, Musik, Musik Daerah, Musik dan Budaya, Musik dan Budaya Thailand, Musik dan Irama, Musik dan Sastra, Musik dan Suara, Musik Eksperimental, Musik Indonesia, Musik Perjuangan, Musik Tradisional, Musik Tradisional Indonesia, Musik Vokal, Nama Bayi, Narkoba, Narkotika dan Zat Adiktif, Negara Tetangga Indonesia, Neurologi, Nilai dalam Literatur, Nilai-Nilai Sosial, Norma Sosial, Notasi Musik, Nutrisi, Olahraga, Olahraga Atletik, Olahraga Bela Diri, Olahraga Bola Besar, Olahraga dan Kebugaran, Olahraga dan Kesehatan, Olahraga Dasar, Olahraga Kasti, Olahraga Lari, Olahraga Raket, Olahraga Tim, Olahraga Tradisional, Optik, Organisasi Pemuda, Ornitologi, Pakaian Dalam, Pakaian Renang, Pakan Ternak, Parenting, Pariwisata, Pariwisata ASEAN, Pariwisata Berkelanjutan, Partisipasi Anak, Pekerjaan dan Karir, Pelanggaran Sepak Bola, Pelatihan Vokal, Pelecehan Seksual, Peluang Usaha, Peluncuran Roket, Pemahaman Membaca, Pemanfaatan Dataran Rendah, Pemasangan, Pemasaran, Pemasaran dan Komunikasi, Pemasaran dan Penjualan, Pemasaran dan Periklanan, Pemasaran dan Promosi, Pemasaran Digital, Pemasaran Online, Pemasaran Sosial, Pembangunan Internasional, Pembangunan Karakter, Pembelajaran dan Pengembangan, Pemberantasan Narkoba, Pembuatan Komik, Pembuatan Maket, Pembuatan Situs Web, Pemilu, Pemisahan Campuran, Pemrosesan Data, Penambangan, Penanggalan, Pencak Silat, Pencarian Kerja, Pencernaan, Pendidikan, Pendidikan Bahasa, Pendidikan Kewarganegaraan, Pendidikan Sains, Penegakan Hukum, Penelitian, Penelitian dan Jurnalisme, Penemuan Informasi, Penerbangan, Pengajaran dan Edukasi, Pengambilan Keputusan, Pengasuhan Anak, Pengawetan Makanan, Pengecatan, Pengelolaan Data, Pengelolaan Dokumen, Pengelolaan Limbah, Pengelolaan Lingkungan, Pengelolaan Reputasi, Pengemasan, Pengembangan Diri, Pengembangan Karier, Pengembangan Perangkat Lunak, Pengembangan Produk, Penggunaan Energi, Penghematan Energi, Pengobatan Tradisional, Pengolah Kata, Pengolahan Pangan, Pengujian Produk, Pengukuran, Pengumpulan Data, Penjelajahan Geografis, Penulisan, Penulisan Akademik, Penulisan Efektif, Penulisan Ilmiah, Penulisan Informatif, Penulisan Konten, Penulisan Kreatif, Penulisan Lagu, Penulisan Non Fiksi, Penulisan Persuasif, Penulisan Teknis, Penulisan Teks, Penyaringan Air, Penyuntingan Teks, Peralatan Listrik, Peralatan Memasak, Peralatan Olahraga, Peralatan Tenis Meja, Peraturan Softball, Peraturan Tenis Meja, Perawatan Anjing, Perawatan Bayi, Perawatan Furnitur, Perawatan Luka, Perawatan Rambut, Perbaikan Usaha, Perdagangan Internasional, Perekonomian, Perekrutan, Perencanaan dan Pengembangan Kegiatan, Perencanaan Hidup, Perikanan, Periklanan, Perilaku dan Nilai, Perilaku Konsumen, Perilaku Manusia, Perilaku Pelajar, Perjalanan, Perkembangan Anak, Perkembangan Anak dan Remaja, Perkembangan Manusia, Perkembangan Pribadi, Perkembangan Remaja, Perlengkapan Rumah, Permainan, Permainan Anak, Permainan dan Aktivitas, Permainan Olahraga, Permainan Tim, Permainan Tradisional, Persahabatan, Persamaan, Persamaan Kuadrat, Persamaan Matematika, Pertahanan Diri, Pertahanan Nasional, Pertambangan, Pertanian, Pertanian dan Masyarakat, Pertanian Laos, Pertemanan, Pertunjukan Seni, Pertunjukan Tari, Perubahan dan Inovasi, Peta Minda, Peternakan, Peternakan dan Pertanian, Petualangan Luar Ruangan, Piano, Pidato, Pola Lantai Tari, Politik, Politik dan Masyarakat, Politik Indonesia, Politik Internasional, Postur Inversi, Praaksara, Produk Dalam Negeri, Produksi, Produksi Kimia, Produksi Tanah Liat, Produksi Teater, Produktivitas, Promosi Budaya Indonesia, Proses Kimia, Proses Produksi, Proses Produksi Buku, Psikologi, Psikologi Sosial, Public Speaking, Puisi, Rangkaian Listrik, Referensi, Renang, Renang Gaya Dada, Renang Gaya Punggung, Reproduksi Manusia, Resensi Buku, Resolusi Konflik, Ritual Islam, Rounders, Ruang Keluarga, Ruang Pameran, Sains, Sastra, Sastra Hewan, Sastra Indonesia, Sastra Jawa, Sastra Klasik Jawa, Sastra Nonfiksi, Sastra Tradisional, Satuan, Satwa Liar, Sayuran, Sejarah, Sejarah Agama, Sejarah Arsitektur, Sejarah dan Budaya Indonesia, Sejarah Hukum, Sejarah Indonesia, Sejarah Industri, Sejarah Internasional, Sejarah Islam, Sejarah Islam di Indonesia, Sejarah Jakarta, Sejarah Keagamaan, Sejarah Kerajaan, Sejarah Perbankan Indonesia, Sejarah Perbudakan, Sejarah Perlawanan Indonesia, Sejarah Praaksara, Sejarah Seni, Sejarah Teknologi, Seleksi dan Rekrutmen, Semiotika, Senam, Senam Irama, Senam Lantai, Seni, Seni Abstrak, Seni Bela Diri, Seni Berpidato, Seni Budaya, Seni dan Apresiasi, Seni dan Budaya, Seni dan Budaya Indonesia, Seni dan Desain, Seni dan Kerajinan, Seni Gerabah, Seni Grafis, Seni Hias, Seni Kerajinan, Seni Komik, Seni Lukis, Seni Musik, Seni Pahat, Seni Patung, Seni Pertunjukan, Seni Pertunjukan Jawa, Seni Pertunjukan Tradisional, Seni Rupa, Seni Rupa Kontemporer, Seni Rupa Pesisir, Seni Tari, Seni Tradisional, Seni Visual, Seni Vokal, Sepak Bola, Serat, Serat Tekstil, Sifat Allah, Sifat dan Perilaku, Sifat Positif, Sistem dan Komponen, Sistem Kelistrikan, Sistem Pencernaan, Sistem Pencernaan Hewan, Sistem Pernapasan, Sistem Politik, Sistem Rangka, Sosiologi, Spiritualitas, Struktur Sastra, Struktur Zat, Studi Sejarah, Suara dan Musik, Suku Indonesia, Sumber Daya Alam, Sumber Energi, Syirkah, Tafsir Al-Qur'an, Tafsir Alquran, Tajwid, Tanaman, Tanaman Pangan, Tanaman Serat, Tanggung Jawab, Tanggung Jawab Sosial Perusahaan, Tantangan Global, Tari, Tari dan Pertunjukan, Tari Kontemporer, Tari Tradisional, Tari Tradisional Indonesia, Tarian, Tarian dan Seni Pertunjukan, Tata Bahasa, Tata Bahasa Indonesia, Tata Bahasa Inggris, Tata Bahasa Jawa, Teater, Teknik, Teknik Baseball, Teknik Bela Diri, Teknik Belajar, Teknik Berenang, Teknik Bernyanyi, Teknik Bola Basket, Teknik Bola Voli, Teknik Bulu Tangkis, Teknik Bulutangkis, Teknik Cetak, Teknik Dasar Olahraga, Teknik Keramik, Teknik Kuliner, Teknik Lari, Teknik Memasak, Teknik Membaca, Teknik Menggambar, Teknik Mengoper Bola, Teknik Menulis, Teknik Musik, Teknik Pencak Silat, Teknik Penulisan, Teknik Pertarungan, Teknik Renang, Teknik Seni, Teknik Sepak Bola, Teknik Tinju, Teknik Vokal, Teknologi, Teknologi Antariksa, Teknologi dalam Seni, Teknologi dan Masyarakat, Teknologi Dapur, Teknologi Inovatif, Teknologi Komputer, Teknologi Mesin, Teks Akademik, Teks Anekdot, Teks Eksplanasi, Teks Ilmiah, Teks Nonfiksi, Teks Prosedur, Tekstil, Tekstil dan Pakaian, Tembang Jawa, Tenaga Kerja, Tenis, Tenis Meja, Teologi, Teologi Islam, Teori Bilangan, Teori Cerita Fantasi, Teori Musik, Teori Sastra, Teori Seni, Teori Warna, Tokoh Agama, Tokoh Inspiratif, Tokoh Islam, Tokoh Mitologi, Tokoh Nasional, Toleransi dan Kerukunan, Tradisi Budaya, Tradisi dan Budaya, Trail Running, Transportasi, Trauma dan Penyembuhan, Tumbuhan Paku, Tutorial, Undangan, Usaha Jasa, Visual Storytelling, Visualisasi, Visualisasi Data, Vokal, Vokal Anak, Wacana Publik, Waktu, Waktu dan Manajemen, Waktu Luang, Warisan Budaya, Wawancara, Wirausaha, Wisata Alam, Wisata Yogyakarta, Yoga, Zakat dan Zoologi.

Persamaan Kuadrat: Temukan Akar yang Tersembunyi di Balik Angka 6