Banyak Titik Pusat pada Lingkaran: Konsep dan Aplikasinya

Banyak titik pusat pada lingkaran adalah – Dalam dunia geometri, lingkaran memiliki banyak titik pusat yang menentukan sifat dan karakteristiknya. Titik pusat lingkaran memainkan peran penting dalam berbagai bidang, mulai dari matematika hingga teknik.

Artikel ini akan mengupas tuntas konsep titik pusat lingkaran, karakteristiknya, cara menemukannya, serta aplikasi menariknya dalam berbagai bidang.

Pengertian Titik Pusat Lingkaran

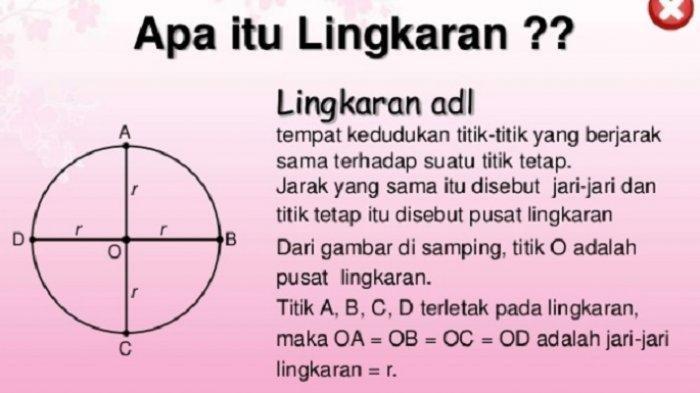
Titik pusat lingkaran merupakan titik tetap yang terletak di tengah lingkaran. Titik ini merupakan pusat simetri dari lingkaran dan jarak dari titik pusat ke setiap titik pada lingkaran selalu sama.

Contohnya, dalam lingkaran dengan jari-jari 5 cm, titik pusatnya terletak di tengah lingkaran dan jarak dari titik pusat ke tepi lingkaran adalah 5 cm.

Menentukan Titik Pusat Lingkaran

Jika diketahui persamaan lingkaran dalam bentuk x²+ y²= r ², maka titik pusatnya adalah (0, 0).
Jika diketahui persamaan lingkaran dalam bentuk (x – h) ²+ (y – k) ²= r ², maka titik pusatnya adalah (h, k).

Sifat Titik Pusat Lingkaran

Titik pusat lingkaran merupakan titik potong dari semua garis sumbu simetri lingkaran.
Jarak dari titik pusat ke setiap titik pada lingkaran selalu sama, yaitu sama dengan jari-jari lingkaran.
Titik pusat lingkaran membagi garis bagi setiap tali busur menjadi dua bagian yang sama panjang.

Karakteristik Titik Pusat Lingkaran

Titik pusat lingkaran merupakan titik tetap yang memiliki jarak sama ke semua titik pada lingkaran. Karakteristik titik pusat lingkaran antara lain:

Posisi Titik Pusat

Terletak di dalam lingkaran.
Membagi lingkaran menjadi dua bagian yang sama (setengah lingkaran).
Berada pada garis lurus yang menghubungkan dua titik manapun pada lingkaran.

Jarak ke Titik pada Lingkaran

Jarak dari titik pusat ke setiap titik pada lingkaran sama, disebut jari-jari (r).
Jarak dari titik pusat ke titik mana pun pada lingkaran sama dengan diameter (d), yang merupakan dua kali jari-jari.

Sudut pada Titik Pusat

Sudut yang dibentuk oleh dua jari-jari yang ditarik dari titik pusat ke dua titik berbeda pada lingkaran adalah sudut pusat.
Sudut pusat mengukur besar busur yang dibatasi oleh kedua jari-jari tersebut.

Cara Menemukan Titik Pusat Lingkaran

Titik pusat lingkaran adalah titik tetap yang menentukan semua sifat lingkaran, termasuk radius dan kelilingnya. Menemukan titik pusat lingkaran sangat penting untuk melakukan berbagai perhitungan dan konstruksi geometris.

Menentukan Titik Pusat Menggunakan Diameter

Diameter adalah garis lurus yang melalui titik pusat lingkaran dan menghubungkan dua titik pada lingkaran. Untuk menemukan titik pusat lingkaran menggunakan diameter, ikuti langkah-langkah berikut:

Tandai dua titik sembarang pada lingkaran.
Hubungkan kedua titik tersebut dengan sebuah garis lurus.
Titik tengah garis lurus tersebut adalah titik pusat lingkaran.

Menentukan Titik Pusat Menggunakan Garis Singgung

Garis singgung adalah garis lurus yang hanya bersinggungan dengan lingkaran pada satu titik. Untuk menemukan titik pusat lingkaran menggunakan garis singgung, ikuti langkah-langkah berikut:

Gambar dua garis singgung ke lingkaran dari titik di luar lingkaran.
Titik potong kedua garis singgung adalah titik pusat lingkaran.

Menentukan Titik Pusat Menggunakan Busur dan Tali

Metode ini menggunakan busur dan tali untuk menentukan titik pusat lingkaran. Berikut langkah-langkahnya:

Pasang tali di busur.
Tempatkan busur pada lingkaran dan gerakkan sehingga tali menyentuh lingkaran pada dua titik.
Tandai titik-titik tersebut pada lingkaran.
Titik tengah garis yang menghubungkan kedua titik tersebut adalah titik pusat lingkaran.

Aplikasi Titik Pusat Lingkaran

Titik pusat lingkaran memiliki berbagai aplikasi dalam berbagai bidang. Titik ini berperan penting dalam menentukan sifat dan karakteristik lingkaran, serta memberikan dasar untuk perhitungan dan analisis geometris.

Dalam Matematika

Titik pusat lingkaran adalah pusat simetri, yang membagi lingkaran menjadi dua bagian yang sama besar dan kongruen. Jarak dari titik pusat ke setiap titik pada lingkaran adalah sama, yang dikenal sebagai jari-jari lingkaran.

Dalam Teknik

Titik pusat lingkaran digunakan dalam desain roda, bantalan, dan mesin putar lainnya. Ini memastikan distribusi beban yang merata dan operasi yang mulus.

Dalam Arsitektur

Titik pusat lingkaran digunakan dalam desain kubah, lengkungan, dan struktur melengkung lainnya. Ini membantu menentukan bentuk dan stabilitas struktur ini.

Dalam Astronomi

Titik pusat lingkaran adalah titik referensi penting dalam astronomi. Orbit planet mengelilingi titik pusat tata surya, dan bintang-bintang berputar mengelilingi titik pusat galaksi.

Dalam Seni dan Desain

Titik pusat lingkaran digunakan dalam desain logo, pola, dan karya seni lainnya. Ini menciptakan rasa keseimbangan, harmoni, dan keteraturan.

Titik Pusat Lingkaran pada Lingkaran Khusus: Banyak Titik Pusat Pada Lingkaran Adalah

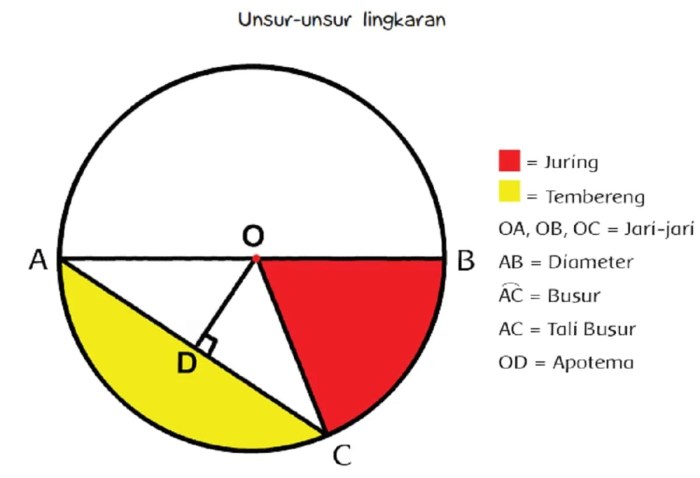
Dalam geometri, lingkaran khusus adalah lingkaran yang memiliki hubungan atau properti tertentu dengan lingkaran lain. Titik pusat lingkaran pada lingkaran khusus ini dapat berbeda dari titik pusat lingkaran biasa.

Lingkaran Berpotongan

Lingkaran berpotongan adalah dua lingkaran yang memiliki dua titik potong. Titik pusat dari kedua lingkaran tidak selalu sama. Titik pusat lingkaran yang lebih besar biasanya berada di luar lingkaran yang lebih kecil.

Lingkaran Singgung, Banyak titik pusat pada lingkaran adalah

Lingkaran singgung adalah dua lingkaran yang bersentuhan di satu titik. Titik pusat kedua lingkaran berada pada garis yang sama yang menghubungkan titik singgung dan titik tengah kedua lingkaran.

Lingkaran Konsentris

Lingkaran konsentris adalah dua atau lebih lingkaran yang memiliki titik pusat yang sama. Semua lingkaran konsentris memiliki jari-jari yang berbeda.

Banyak Titik Pusat pada Lingkaran: Konsep dan Aplikasinya

indoaviation.co.id platform online yang berdedikasi untuk menyediakan informasi yang akurat, terkini, dan relevan dalam berbagai topik menarik seputar manfaat, Administrasi, Agama, Agama dan Kepercayaan, Agama dan Masyarakat, Agama dan Spiritualitas, Agama di Indonesia, Agama Islam, Ajaran Islam, Akhlak, Akhlak Islam, Aktivitas Fisik, Aktivitas Gerak Berirama, Aktivitas Luar Ruangan, Akustik, Alam, Alam dan Lingkungan, Alam dan Satwa Liar, Alat, Alat Musik, Alat Musik Perkusi, Alat Musik Tiup, Alat Optik, Alat Tulis, Aljabar, Amal, Analisis Anekdot, Analisis Bisnis, Analisis Data, Analisis Gambar, Analisis Musik, Analisis Narasi, Analisis Percakapan, Analisis Puisi, Analisis Sastra, Analisis Teks, Anatomi, Anatomi Kardiovaskular, Anime dan Manga, Antropologi, Antropologi Budaya, Aplikasi, Arkeologi, Arsitektur, Arsitektur Buddha, Asmaul Husna, Astronomi, Atletik, Aturan Sepak Bola, Bacaan Al-Qur'an, Bahan, Bahan Alami, Bahan Baku Tekstil, Bahan Bangunan, Bahan Kemasan, Bahan Lanjutan, Bahan Makanan, Bahan Tambahan Makanan, Bahan Tekstil, Bahasa, Bahasa Arab, Bahasa Daerah, Bahasa dan Budaya, Bahasa dan Budaya Jepang, Bahasa dan Komunikasi, Bahasa dan Linguistik, Bahasa dan Masyarakat, Bahasa dan Sastra, Bahasa Indonesia, Bahasa Inggris, Bahasa Jawa, Batik, Belajar, Belajar Efektif, Belanja, Benda Langit, Berenang, Berita dan Media, Berkebun, Berkemah dan Mendaki, Berkuda, Bernyanyi, Bibliografi, Biokimia, Biologi, Biologi Hewan, Biologi Populasi, Biologi Sel, Biologi Tumbuhan, Bioteknologi, Bisbol, Bisnis dan Ekonomi, Bisnis dan Kewirausahaan, Bisnis Pertanian, Bola Basket, Bola Voli, Botani, Branding, Buah-buahan, Budaya, Budaya Aceh, Budaya Betawi, Budaya Daerah, Budaya dan Filsafat, Budaya dan Masyarakat, Budaya dan Tradisi, Budaya Indonesia, Budaya Jawa, Budaya Kalimantan Barat, Budidaya Buah, Budidaya Hewan, Budidaya Perikanan, Bulutangkis, Bumbu dan Rempah, Cara, Ceramah dan Presentasi, Ciptaan Tuhan, Dampak Globalisasi, Dekorasi Rumah, Demokrasi, Desain Buku, Desain Grafis, Desain Interior, Desain Poster, Desain sampul buku, Desain Warna, Distribusi, Dokumen, Dokumentasi Proses, Dongeng, Dongeng dan Makna Hidup, Dunia Hewan, Ekologi, Ekologi dan Konservasi, Ekologi Tanah, Ekologi Tumbuhan, Ekonomi, Ekonomi ASEAN, Ekonomi Asia Tenggara, Ekonomi Bisnis, Ekonomi dan Bisnis, Ekonomi Global, Ekonomi Indonesia, Ekonomi Pedesaan, Ekonomi Pertanian, Ekonomi Singapura, Eksplorasi Luar Angkasa, Elektronik, Elektronika, Energi, Energi Bersih, Energi Terbarukan, Entomologi, Ergonomi, Eropa, Eskatologi Islam, Estetika, Etika, Etika dan Moral, Etika dan Moralitas, Etika dan Nilai-Nilai, Falsafah Pancasila, Fantasi, Fashion, Fashion dan Desain, Fashion dan Gaya Hidup, Fenomena Alam, Fenomena Global, Fiksi, Fiksi Ilmiah, Filosofi Hidup, Filosofi Kehidupan, Filsafat, Filsafat dan Spiritualitas, Filsafat Hidup, Filsafat Jawa, Filsafat Politik, Finishing Perabot, Fisika, Fisika Akustik, Fisika Bola, Fisika Dasar, Fisika Optik, Fisika Suara, Fisika Terapan, Fisika Termal, Fisiologi Hewan, Flora dan Fauna, Fonologi, Formulir, Fotografi, Fungsi Ekologis Hutan, Furnitur, Game Strategi, Gangguan Darah, Gangguan Pencernaan, Gaya, Genetika Manusia, Geografi, Geografi Afrika, Geografi Asia, Geografi Asia Tenggara, Geografi Jepang, Geografi Sosial, Geometri, Geometri Lingkaran, Geosains, Gerak Berirama, Gerak Tari, Gerakan Tubuh, Globalisasi, Habitat Tanaman, Hadis, Hak Asasi Manusia, Hak dan Kewajiban, Hak Kekayaan Intelektual, Hak Warga Negara, Hak-hak Asasi Manusia, Hasil Hutan, Hemat Energi, Hewan, Hewan Gurun, Hewan Liar, Hubungan, Hubungan Internasional, Hubungan Interpersonal, Hubungan Keluarga, Hubungan Sosial, Hukum, Hukum Bacaan Alquran, Hukum Bisnis, Hukum dan Masyarakat, Hukum Konstitusi, Hukum Tata Negara, Hutan, Ibadah, Ibadah dan Amaliah Keagamaan, Identitas Pribadi, Ideologi Bangsa, Iklan, Iklan dan Pemasaran, Ilmu Material, Ilmu Pengetahuan, Ilmu Pengetahuan Alam, Ilmu Pengetahuan dan Kehidupan Manusia, Ilmu Sosial, Ilmu Tajwid, Ilustrasi, Ilustrasi Digital, Iman, Industri, Industri Makanan, Industri Tekstil, Informasi dan Literasi, Infrastruktur Pejalan Kaki, Inspirasi, Interaksi Manusia, Interaksi Sosial, Interpretasi Gambar, Investasi Emas, Jujutsu Kaisen, Jurnalisme, Karakter dan Etika, Karakter Fiksi, Kartografi, Karya Sastra, Keamanan Listrik, Keamanan Siber, Kearifan Lokal, Kebanggaan Nasional, Keberagaman dan Inklusi, Keberagaman dan Integrasi, Kebersihan, Kebijaksanaan, Kebugaran, Kebugaran dan Kesehatan, Kebugaran dan Latihan, Kebugaran dan Olahraga, Kebugaran Fisik, Kebugaran Jasmani, Kebutuhan Remaja, Kegiatan Ekonomi, Kegiatan Sosial, Kehidupan, Kehidupan Beragama, Kehidupan Berbangsa dan Bernegara, Kehidupan Bermasyarakat, Kehidupan Bertetangga, Kehidupan Desa, Kehidupan Keluarga, Kehidupan Satwa Liar, Kehidupan Sehari-hari, Kehidupan Sosial, Keimanan, Keindahan Alam, Keislaman, Kekerasan Seksual, Kelestarian Lingkungan, Kelincahan Olahraga, Kelistrikan, Keluarga, Kemagnetan, Kemajemukan, Kemasan Produk, Kenabian, Kenampakan Alam, Kepedulian Sosial, Kepemimpinan, Kepemimpinan Islami, Kependudukan, Kepercayaan Agama, Kepercayaan dan Spiritualitas, Kerajinan, Kerajinan Tangan, Kerajinan Tradisional, Keramik, Kerja Sama Internasional, Kerjasama ASEAN, Kerjasama Regional, Kesehatan, Kesehatan dan Kebugaran, Kesehatan dan Keselamatan, Kesehatan dan Lingkungan, Kesehatan dan Nutrisi, Kesehatan Gigi, Kesehatan Kaki, Kesehatan Lingkungan, Kesehatan Masyarakat, Kesehatan Mental, Kesehatan Muskuloskeletal, Kesehatan Pernapasan, Kesehatan Sendi, Kesehatan Tanaman, Kesehatan Tenggorokan, Kesehatan Tulang, Kesejahteraan Hewan dan Tumbuhan, Kesejahteraan Masyarakat, Kesenian Tradisional, Ketahanan Nasional, Ketahanan Negara, Ketahanan Pangan, Keterampilan Basket, Keterampilan Berbahasa, Keterampilan Berbicara, Keterampilan Berkomunikasi, Keterampilan Komunikasi, Keterampilan Membaca, Keterampilan Menulis, Keterampilan Olahraga, Keterampilan Sepak Bola, Keuangan, Kewajiban Agama, Kewajiban dan Tanggung Jawab, Kewarganegaraan, Keyakinan Islam, Khotbah, Kimia, Kimia Anorganik, Kimia Dasar, Kimia Fisika, Kisah Alkitab, Kisah Nabi, Komunikasi, Komunikasi Digital, Komunikasi Efektif, Komunikasi Interpersonal, Komunikasi Publik, Komunikasi Verbal, Komunikasi Visual, Komunitas, Konflik, Konflik Sosial, Konservasi Alam, Konservasi Energi, Konservasi Satwa Liar, Konservasi Sumber Daya Alam, Konservasi Tanah, Konstruksi dan Bangunan, Konversi, Konversi Satuan, Konversi Unit, Konversi Waktu, Koperasi dan Pertanian, Koreografi, Koreografi Tari, Kosmologi, Kritik Sastra, Kuda-Kuda, Kuliner, Kuliner Indonesia, Kursi, Laporan Ilmiah, Lari, Lari Cepat, Lari Jarak Jauh, Lari Jarak Pendek, Latihan Fisik, Latihan Kebugaran, Latihan Kekuatan, Latihan Olahraga, Latihan Sepak Bola, Legenda, Legenda Rakyat Indonesia, Lembaga Sosial, Lilin, Limbah Industri, Lingkungan, Lingkungan dan Masyarakat, Lingkungan Hidup, Linguistik, Literasi Media, Lukisan, Mahabharata, Mainan kucing, Majas, Makanan, Makanan Cepat Saji, Makanan dan Minuman, Malaikat, Mamalia Indonesia, Manajemen Acara, Manajemen Bisnis, Manajemen Data, Manajemen Diri, Manajemen Keuangan, Manajemen Kualitas, Manajemen Organisasi, Manajemen Pameran, Manajemen Pelayanan, Manajemen Perubahan, Manajemen Waktu, Manajemen Wawancara, Manfaat, Manfaat Membaca, Manufaktur, Manusia dan Masyarakat, Masakan Indonesia, Masalah Sosial ASEAN, Masyarakat, Mata Uang, Matematika, Matematika Dasar, Media Elektronik, Media Seni Musik, Melukis, Memahami Teks, Memasak, Membaca dan Menulis, Menembak, Menggambar, Menggambar Komik, Menulis, Menulis Cerpen, Menulis Kreatif, Metabolisme Hewan, Metalurgi, Meteorologi, Metodologi Penelitian, Migrasi, Mineral dan Penambangan, Miniatur, Mitologi Hindu, Moralitas, Motif Ekonomi, Motif Geometris, Motivasi Diri, Musik, Musik Daerah, Musik dan Budaya, Musik dan Budaya Thailand, Musik dan Irama, Musik dan Sastra, Musik dan Suara, Musik Eksperimental, Musik Indonesia, Musik Perjuangan, Musik Tradisional, Musik Tradisional Indonesia, Musik Vokal, Nama Bayi, Narkoba, Narkotika dan Zat Adiktif, Negara Tetangga Indonesia, Neurologi, Nilai dalam Literatur, Nilai-Nilai Sosial, Norma Sosial, Notasi Musik, Nutrisi, Olahraga, Olahraga Atletik, Olahraga Bela Diri, Olahraga Bola Besar, Olahraga dan Kebugaran, Olahraga dan Kesehatan, Olahraga Dasar, Olahraga Kasti, Olahraga Lari, Olahraga Raket, Olahraga Tim, Olahraga Tradisional, Optik, Organisasi Pemuda, Ornitologi, Pakaian Dalam, Pakaian Renang, Pakan Ternak, Parenting, Pariwisata, Pariwisata ASEAN, Pariwisata Berkelanjutan, Partisipasi Anak, Pekerjaan dan Karir, Pelanggaran Sepak Bola, Pelatihan Vokal, Pelecehan Seksual, Peluang Usaha, Peluncuran Roket, Pemahaman Membaca, Pemanfaatan Dataran Rendah, Pemasangan, Pemasaran, Pemasaran dan Komunikasi, Pemasaran dan Penjualan, Pemasaran dan Periklanan, Pemasaran dan Promosi, Pemasaran Digital, Pemasaran Online, Pemasaran Sosial, Pembangunan Internasional, Pembangunan Karakter, Pembelajaran dan Pengembangan, Pemberantasan Narkoba, Pembuatan Komik, Pembuatan Maket, Pembuatan Situs Web, Pemilu, Pemisahan Campuran, Pemrosesan Data, Penambangan, Penanggalan, Pencak Silat, Pencarian Kerja, Pencernaan, Pendidikan, Pendidikan Bahasa, Pendidikan Kewarganegaraan, Pendidikan Sains, Penegakan Hukum, Penelitian, Penelitian dan Jurnalisme, Penemuan Informasi, Penerbangan, Pengajaran dan Edukasi, Pengambilan Keputusan, Pengasuhan Anak, Pengawetan Makanan, Pengecatan, Pengelolaan Data, Pengelolaan Dokumen, Pengelolaan Limbah, Pengelolaan Lingkungan, Pengelolaan Reputasi, Pengemasan, Pengembangan Diri, Pengembangan Karier, Pengembangan Perangkat Lunak, Pengembangan Produk, Penggunaan Energi, Penghematan Energi, Pengobatan Tradisional, Pengolah Kata, Pengolahan Pangan, Pengujian Produk, Pengukuran, Pengumpulan Data, Penjelajahan Geografis, Penulisan, Penulisan Akademik, Penulisan Efektif, Penulisan Ilmiah, Penulisan Informatif, Penulisan Konten, Penulisan Kreatif, Penulisan Lagu, Penulisan Non Fiksi, Penulisan Persuasif, Penulisan Teknis, Penulisan Teks, Penyaringan Air, Penyuntingan Teks, Peralatan Listrik, Peralatan Memasak, Peralatan Olahraga, Peralatan Tenis Meja, Peraturan Softball, Peraturan Tenis Meja, Perawatan Anjing, Perawatan Bayi, Perawatan Furnitur, Perawatan Luka, Perawatan Rambut, Perbaikan Usaha, Perdagangan Internasional, Perekonomian, Perekrutan, Perencanaan dan Pengembangan Kegiatan, Perencanaan Hidup, Perikanan, Periklanan, Perilaku dan Nilai, Perilaku Konsumen, Perilaku Manusia, Perilaku Pelajar, Perjalanan, Perkembangan Anak, Perkembangan Anak dan Remaja, Perkembangan Manusia, Perkembangan Pribadi, Perkembangan Remaja, Perlengkapan Rumah, Permainan, Permainan Anak, Permainan dan Aktivitas, Permainan Olahraga, Permainan Tim, Permainan Tradisional, Persahabatan, Persamaan, Persamaan Kuadrat, Persamaan Matematika, Pertahanan Diri, Pertahanan Nasional, Pertambangan, Pertanian, Pertanian dan Masyarakat, Pertanian Laos, Pertemanan, Pertunjukan Seni, Pertunjukan Tari, Perubahan dan Inovasi, Peta Minda, Peternakan, Peternakan dan Pertanian, Petualangan Luar Ruangan, Piano, Pidato, Pola Lantai Tari, Politik, Politik dan Masyarakat, Politik Indonesia, Politik Internasional, Postur Inversi, Praaksara, Produk Dalam Negeri, Produksi, Produksi Kimia, Produksi Tanah Liat, Produksi Teater, Produktivitas, Promosi Budaya Indonesia, Proses Kimia, Proses Produksi, Proses Produksi Buku, Psikologi, Psikologi Sosial, Public Speaking, Puisi, Rangkaian Listrik, Referensi, Renang, Renang Gaya Dada, Renang Gaya Punggung, Reproduksi Manusia, Resensi Buku, Resolusi Konflik, Ritual Islam, Rounders, Ruang Keluarga, Ruang Pameran, Sains, Sastra, Sastra Hewan, Sastra Indonesia, Sastra Jawa, Sastra Klasik Jawa, Sastra Nonfiksi, Sastra Tradisional, Satuan, Satwa Liar, Sayuran, Sejarah, Sejarah Agama, Sejarah Arsitektur, Sejarah dan Budaya Indonesia, Sejarah Hukum, Sejarah Indonesia, Sejarah Industri, Sejarah Internasional, Sejarah Islam, Sejarah Islam di Indonesia, Sejarah Jakarta, Sejarah Keagamaan, Sejarah Kerajaan, Sejarah Perbankan Indonesia, Sejarah Perbudakan, Sejarah Perlawanan Indonesia, Sejarah Praaksara, Sejarah Seni, Sejarah Teknologi, Seleksi dan Rekrutmen, Semiotika, Senam, Senam Irama, Senam Lantai, Seni, Seni Abstrak, Seni Bela Diri, Seni Berpidato, Seni Budaya, Seni dan Apresiasi, Seni dan Budaya, Seni dan Budaya Indonesia, Seni dan Desain, Seni dan Kerajinan, Seni Gerabah, Seni Grafis, Seni Hias, Seni Kerajinan, Seni Komik, Seni Lukis, Seni Musik, Seni Pahat, Seni Patung, Seni Pertunjukan, Seni Pertunjukan Jawa, Seni Pertunjukan Tradisional, Seni Rupa, Seni Rupa Kontemporer, Seni Rupa Pesisir, Seni Tari, Seni Tradisional, Seni Visual, Seni Vokal, Sepak Bola, Serat, Serat Tekstil, Sifat Allah, Sifat dan Perilaku, Sifat Positif, Sistem dan Komponen, Sistem Kelistrikan, Sistem Pencernaan, Sistem Pencernaan Hewan, Sistem Pernapasan, Sistem Politik, Sistem Rangka, Sosiologi, Spiritualitas, Struktur Sastra, Struktur Zat, Studi Sejarah, Suara dan Musik, Suku Indonesia, Sumber Daya Alam, Sumber Energi, Syirkah, Tafsir Al-Qur'an, Tafsir Alquran, Tajwid, Tanaman, Tanaman Pangan, Tanaman Serat, Tanggung Jawab, Tanggung Jawab Sosial Perusahaan, Tantangan Global, Tari, Tari dan Pertunjukan, Tari Kontemporer, Tari Tradisional, Tari Tradisional Indonesia, Tarian, Tarian dan Seni Pertunjukan, Tata Bahasa, Tata Bahasa Indonesia, Tata Bahasa Inggris, Tata Bahasa Jawa, Teater, Teknik, Teknik Baseball, Teknik Bela Diri, Teknik Belajar, Teknik Berenang, Teknik Bernyanyi, Teknik Bola Basket, Teknik Bola Voli, Teknik Bulu Tangkis, Teknik Bulutangkis, Teknik Cetak, Teknik Dasar Olahraga, Teknik Keramik, Teknik Kuliner, Teknik Lari, Teknik Memasak, Teknik Membaca, Teknik Menggambar, Teknik Mengoper Bola, Teknik Menulis, Teknik Musik, Teknik Pencak Silat, Teknik Penulisan, Teknik Pertarungan, Teknik Renang, Teknik Seni, Teknik Sepak Bola, Teknik Tinju, Teknik Vokal, Teknologi, Teknologi Antariksa, Teknologi dalam Seni, Teknologi dan Masyarakat, Teknologi Dapur, Teknologi Inovatif, Teknologi Komputer, Teknologi Mesin, Teks Akademik, Teks Anekdot, Teks Eksplanasi, Teks Ilmiah, Teks Nonfiksi, Teks Prosedur, Tekstil, Tekstil dan Pakaian, Tembang Jawa, Tenaga Kerja, Tenis, Tenis Meja, Teologi, Teologi Islam, Teori Bilangan, Teori Cerita Fantasi, Teori Musik, Teori Sastra, Teori Seni, Teori Warna, Tokoh Agama, Tokoh Inspiratif, Tokoh Islam, Tokoh Mitologi, Tokoh Nasional, Toleransi dan Kerukunan, Tradisi Budaya, Tradisi dan Budaya, Trail Running, Transportasi, Trauma dan Penyembuhan, Tumbuhan Paku, Tutorial, Undangan, Usaha Jasa, Visual Storytelling, Visualisasi, Visualisasi Data, Vokal, Vokal Anak, Wacana Publik, Waktu, Waktu dan Manajemen, Waktu Luang, Warisan Budaya, Wawancara, Wirausaha, Wisata Alam, Wisata Yogyakarta, Yoga, Zakat dan Zoologi.

Banyak Titik Pusat pada Lingkaran: Konsep dan Aplikasinya